Let us now get into mathematics. Who would have ever thought that alphabets would still find themselves in mathematical formulas and functions?
An equation is simply defined as equality with different variables also known as unknowns which may be more than just two. The variables or the unknowns are usually represented by letters of the alphabet.
Having an equation means it needs solving, which may not be correct at all times, but we solve equations by finding out the identity or representations of the variables that will make the equation true.
Equations are divided into two parts; the first part of the equation is to the left side before the equal sign while the other side comes after the equal mark on the right-hand side.
The equation may be in two forms, the first form may contain what we term as identity equation within which the variables are true for all values of the variables whereas the conditional equations may only be true for variables of a particular value.
Without the equal sign, an expression will cease to be an equation. Here is an example of a general equation:
X2 + 3b + 234 = 5
See Also: 26 Different Types of Math
Types of Equations
1. Polynomial Equation
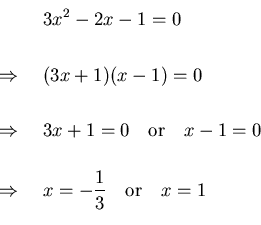
Polynomial equations will only contain positive integer exponents that have been set to equal zero. A polynomial equation is an algebraic equation and is written in the form: X = y
Whereby x and y are polynomials with coefficients that are real numbers.
Polynomial equations may also contain more than one variables, for example:
X2 + 3b + 234 = 0
2. Rational Polynomial Equation
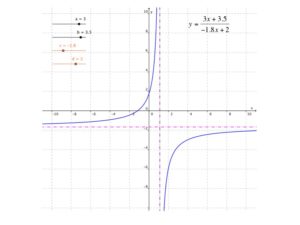
A rational polynomial equation is simply an algebraic equations containing rations.
An example of a rational polynomial equation is:
x/2 = [x + 2] / 4
3. Irrational Polynomial Equation

An irrational equation may contain a variable as a radical or a base of power with a fractional exponent.
An example of an irrational exponent is:
√ [x – 2] = 2x + 1
Such equations are solved by raising the equations to same power on both sides of the equation or through introducing a new variable.
Related: 7 Different Types of Fractions
4. Transcendental Equation
A transcendental equation is an equation containing the transcendental functions of which the variables are to be solved for.
An example of a transcendental equation is:
X = e-x
X = cos x
Transcendental equations are solved through inverse functions.
5. Linear Equation
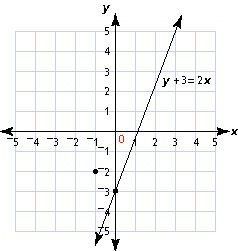
These are equations for straight lines.
One thing to note about linear equations is that when they contain two variables their graph is always plotted in a straight line. Each term in a linear equation is a constant or is the product of a constant and a variable.
There are many ways within which linear equations may be written yet one factor stands that they should contain a constant c and easy variables like x and y. The variables, however, lack exponents and neither do they have squares no square roots.
An example of a linear equation is:
Y = mx + c
In this typical example, m is always known as the slope, whereas c is the point within the curve that it cuts the y axis. A linear equation may be in three forms:
One variable:
8x – 7 = 0
Two variables:
45x + 5j = 456
Three variables:
6y + 7l – 6t = 68
6. Quadratic Equation
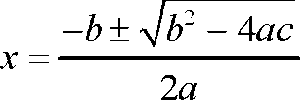
A quadratic equation will simply have an exponent of two on the variable as shown in the example below:
X2 + 3x + 234 = 0
There is a general formula used in finding the roots of the general quadratic equation as the one shown above:
x= (-b ± √(b^2 – 4ac))/2a
Whereby with reference to the given example a = 1, b = 3 and c = 234.
The quadratic equations may be solved through factorizing methods or completing the square method or using the quadratic formula to substitute for the values given in the equation.
7. Trigonometric Equation
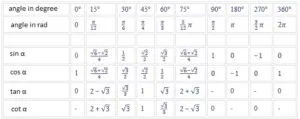
A trigonometric equation is just any equation that contains a trigonometric function. All trigonometric equations holding true for any angles is known as a trigonometric identity.
A few trigonometric equations may be performed or solved without the use of a calculator whereas the rest may be too complex not to use a calculator.
An example of a trigonometric equation is:
Tan [x] = 3.2
8. Radical Equation

Radical equations have what we call exponents and we know or identify a radical equation due to the fact that its exponent on the variable is usually ½ or a square root.
An example of a radical equation is:
√[x] + 10 = 26
9. Exponential Equation

There are some equations that instead of having real exponentials, they have variables instead. The exponential equations have variable as exponents.
For example:
Xy – ab = 78
10. Cubic Equation

A cubic equation is simply an equation with a cubic polynomial in that one of the variable has a cubic exponential.
An example of a cubic equation is:
X3 + ax2 + x +a = 0

